本文最后更新于:1 年前
例子均使用c++实现。
(一)汉诺塔问题:
1. 问题:
汉诺塔问题是一个经典的问题。该问题是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置n个盘子。
问题的目标是把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。
操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
2. 基本思想:
假设共需要移动A柱的n个盘子。
首先考虑最大的盘子,如果移到B柱,未来仍需要移动到C柱,等于直接从A柱移到C柱,所以可以省略无用的这一步,直接从A->C,那么其他的n-1个盘子应当为其腾出空间移动,移动至B柱,否则此步无法进行。等待最大的移动到C柱之后将这n-1个盘子其移动到C柱,而此过程可以看作新的汉诺塔问题:从B柱到C柱移动n-1个盘子,问题性质不变.......直到只剩最小的盘子,此时可以直接移到C柱,问题的解是显然的。
由上面的过程和性质,汉诺塔问题显然可以分治解决,将一个复杂的N问题一步步分解为子问题,直到变成1问题,1问题的解是直观的,再逐步合并子问题,得到原问题的解。
3. 时间复杂度:
设盘子个数为n时,需要T(n)步,把A柱子n-1个盘子移到B柱子,需要T(n-1)步,而A柱子最后一个盘子移到C柱子1步,B柱子上n-1个盘子移到C柱子上T(n-1)步。进而可得公式:
T(n)=2T(n-1)+1
所以汉诺塔问题的时间复杂度为O(2n);
4. 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include<iostream>
using namespace std;
void tower_of_Hanoi(int n, char a, char b, char c)
{
if (n == 1)
{
cout << "第1个盘子由" << a << "->" << c << endl;
}
else
{
tower_of_Hanoi(n - 1, a, c, b);
cout << "第" << n << "个盘子由" << a << "->" << c << endl;
tower_of_Hanoi(n - 1, b, a, c);
}
return;
}
int main()
{
tower_of_Hanoi(16,'A','B','C');
return 0;
}
|
(二)有序二分查找问题:
1. 问题:
在某一个有序序列内查找某个值是否存在。
2. 基本思想:
二分查找算法,也称折半搜索算法、对数搜索算法,是一种在有序数组中查找某一特定元素的分治搜索算法。
二分查找算法有许多中变种。比如分散层叠可以提升在多个数组中对同一个数值的搜索,指数搜索将二分查找算法拓宽到无边界的列表。二叉搜索树和B树数据结构就是基于二分查找算法的。
二分查找算法的搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
我们假设查询对象是一个名为array的数组,且为升序排序,使用变量left表示查找范围的左边界,right表示右边界,mid表示中间位置(向下取整),value为要查找的元素。二分查找算法的实现过程如下:
-
初始化数组array的值(有序升序排序)。
left=0,指向array[ ]的第一个元素。
right=array.length-1,指向数组array[ ]的最后一个元素。
mid=(left+right) / 2,即指向查找范围的中间元素,且向下取整。
-
判定 left<=right是否成立,如果不成立,算法结束,说明该列表中没有指定元素。
-
如果2中判断成立,比较value和 array[mid] 。如果 value == array[mid] ,搜索成功,算法结束,返回相对应的位置或者布尔值;如果 value >array[mid] ,令 left=mid+1,并更新mid=(left+right) / 2,继续在数组的后半部分进行搜索,重复2和3步即可;如果 value <array[mid] ,令 right=mid-1,同样更新mid,继续在数组的前半部分进行搜索,重复2和3步即可。
3. 时间复杂度:
二分查找每次会使得查找区间缩小一半,从n到n/2,n/4,…,n/2^k。
k为循环的次数,最坏情况下k次二分之后在区间长度为1时找到了需要的元素。
则有:n/2k=1 ,可得 k=log2n,
故复杂度为 O(logn);
二分查找算法在一般情况下的复杂度是对数时间并使用常数空间,无论对任何大小的输入数据,算法使用的空间都是一样的。
除非输入数据数量很少,否则二分查找算法比线性搜索更快,但数组必须事先被排序。尽管特定的、为了快速搜索而设计的数据结构更有效(比如哈希表),但二分查找算法应用面更广。
4. 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<iostream>
#include <ctime>
#include <random>
#include<vector>
#include<algorithm>
using namespace std;
int search_binary(vector<int>v, int value)
{
int left = 0;
int right = v.size() - 1;
int mid = left + right >>1;
while (left <= right)
{
if (v[mid] == value)
{
return mid;
}
else if (value < v[mid])
{
right = mid - 1;
}
else
{
left = mid + 1;
}
mid = left + right >> 1;
}
cout << "未查询到结果!!!" << endl;
return -1;
}
int main()
{
std::default_random_engine e;
std::uniform_int_distribution<int> u(1, 200);
e.seed(time(0));
vector<int>v;
for (int i = 0; i < 50; i++)
{
int j = u(e);
v.push_back(j);
}
sort(v.begin(),v.end());
for (int i = 0; i < 10; i++) {
cout << search_binary(v, 50 + i) << endl;;
}
return 0;
}
|
(三)归并排序:
1. 问题:
2. 基本思想:
3. 时间复杂度:
4. 代码:
(四)快速排序:
1. 问题:
2. 基本思想:
3. 时间复杂度:
4. 代码:
(五)线性时间选择(无序二分查找):
1. 问题:
给定线性序集中n个元素(元素不重复)和一个整数k,1≤k≤n,要求找出这n个元素中第k小的元素。
2. 基本思想:
使用线性时间选择算法Select(),此方法实际上是从快速排序方法上改进而来的。
此算法常使用的场景是:找出待排序序列中, 第k大或第k小元素(1<k<n)。此种算法常用于待排序序列>75时,因为元素个数75时,时间复杂度很低,可以直接进行冒泡排序返回arr[n-k+1]。
步骤为:
-
将n个输入元素划分成n/5(向上取整)个组,每组5个元素,最多只可能有一个组不是5个元素。用任意一种排序算法,将每个元素数量为5的组的元素排好序,同时依次将每组的中位数(第三小的元素)与该序列进行元素交换到序列最前方(以便于后续求中位数的中位数),中位数数量共n/5(向下取整)个。
-
求出序列开始处这n/5(向下取整)个元素的中位数。如果n/5(向下取整)是偶数,就找它的2个中位数中较大的一个。
-
将这个最终的中位数交换到序列最开始的地方,并以这个元素作为划分基准,遍历全序列进行划分,用两个指针从开始处和结尾处不断将前面比这个元素大的和后面比这个元素小的数进行交换(优先移动后面的指针,这样保证两个指针相遇时指向的值比划分元素小),直到两个指针相遇,随后将划分元素和指针指向的元素交换。
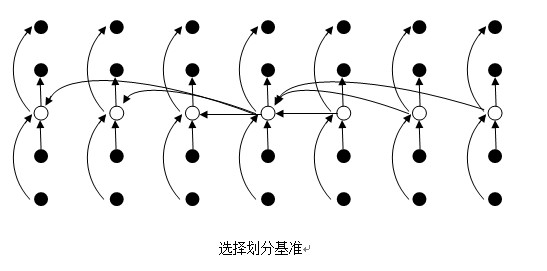
-
此时根据此划分元素位置pos可以确定其为第pos+1小的元素,进行pos+1和k的比较,如果相等,返回划分元素即为答案;如果k<pos+1,对划分元素左侧进行递归处理(即为子问题),如果k>pos+1,对划分元素右侧进行递归处理。
3. 时间复杂度:
线性时间选择算法划分的基准是固定的,可以在线性时间内找到一个划分基准并完成划分。
对于线性时间选择算法每次选择的划分元素,能够确定比划分元素大的数包括比它大的中位数,和这些中位数所在组的比这些中位数大的数,约占整个数组的3/10(1/2*3/5),确定比划分元素小的数的数量同理。——这也就是说,即使在最恶劣的情况下,也可以每次丢弃3/10的元素进行子问题的递归处理。
由此可得复杂度的递推公式:
T(n) = T(3n/10)+O(n)
由主方法,可解得
T(n) =O(n)
4. 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
| #include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
void bubbleSort(vector<int>&a, int p, int r)
{
for (int i = p; i < r; i++)
{
for (int j = i + 1; j <= r; j++)
{
if (a[j] < a[i])
swap(a[i], a[j]);
}
}
}
int Partition(vector<int> &a, int p, int r, int val)
{
int pos=0;
for (int q = p; q <= r; q++)
{
if (a[q] == val)
{
pos = q;
break;
}
}
swap(a[p], a[pos]);
int midmidpos;
int i = p, j = r + 1, midmid = a[p];
while (1)
{
while (a[--j] > midmid && j > p+1);
while (a[++i] < midmid);
if (i >= j) { break; }
swap(a[i], a[j]);
}
a[p] = a[j];
a[j] = midmid;
midmidpos = j;
return midmidpos;
}
int Select(vector<int> &a, int p, int r, int k)
{
if (r - p < 75)
{
bubbleSort(a, p, r);
return a[p + k - 1];
}
for (int i = 0; i <= (r - p - 4) / 5; i++)
{
int s = p + 5 * i, t = s + 4;
for (int j = 0; j < 3; j++)
{
for (int n = s; n < t - j; n++)
{
if (a[n] > a[n + 1])
swap(a[n+1], a[n]);
}
}
swap(a[p + i], a[s + 2]);
}
int midmid = Select(a, p, p + (r - p - 4) / 5, (r - p + 1) / 10);
int midmidpos = Partition(a, p, r, midmid);
int realmidmidpos = midmid - p + 1;
if (k <= realmidmidpos)return Select(a, p, midmidpos-1, k);
else return Select(a, midmidpos + 1, r , k - realmidmidpos);
}
int main()
{
int x;
vector<int> a;
for(int i=1;i<=1000;i++)
{
a.push_back(i);
}
random_shuffle(a.begin(), a.end());
for(int i=0;i<15;i++)
{
vector<int> aa = a;
cout << "第" << i + 1 << "小的数是:" << Select(aa,0,777,i+1)<<endl;
}
return 0;
}
|
(六)大整数乘法:
(七)Strassen矩阵乘法:
(八)循环赛日程表:
(九)最近点对问题:
(十)棋盘覆盖:
